Stack in Python

The stack is a linear data structure that will allow adding or removing elements in a particular order. When a new element is added at one end, it goes on the top of the stack. Stack follows the “Last in First out” order. In stack, we can add, traverse, and remove the elements at the same end only. Ex: Pile of objects.

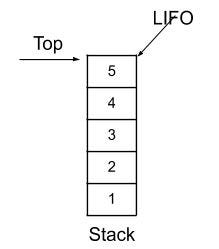
Basic Features:

• push() is used to insert a new element.
• pop() is used to delete the top element.
• It does not have any fixed size but the size() function is used to return the size of the stack.
• empty() will return whether the stack is empty or not.
• full() will return whether the stack is full in size or not.

Implementation in Python:

There are three ways to implement stack using python.

(i) List:

In python, a list can be used as a stack. Instead of using push(), append() is used to add new elements to the top of the stack, and pop() is for removing an element from the top of the stack.
Let’s create an empty list called lis and add a,b,c by using the append() function at the top of the stack.

lis = []
lis.append('a')
lis.append('b')
lis.append('c')

Now, to view the elements inside the stack with the help of the print function and remove the top element of the stack by using the pop() function and finally print the stack.

print(“First pop: “,end=””)
print(lis.pop())
print(“Second pop: “,end=””)
print(lis.pop())
print(“Third pop: “,end=””)
print(lis.pop())

Please find the code below,

Output:

(ii) Collections Module:

In this collections module, the deque class acts as a stack. Here also, append() and pop() functions are used to add or remove elements in the stack.

Here, we have imported the deque class from the collections module and created an object called lis1.

Output:

(iii) Queue Module:

In this queue module, the LifoQueue class acts as a stack. Here, put() and get() functions are used to add or remove elements in the stack.

Here, we have imported the LifoQueue class from the queue module and created an object called lis2 with a maximum size of 3. Add a,b,c by using the put() function at the top of the stack, and for removing we used the get() function.

lis2.put(‘a’)
lis2.put(‘b’)
lis2.put(‘c’)

print(lis2.get())
print(lis2.get())
print(lis2.get())

print(lis2.qsize()) - It prints the size of the stack.
print(lis2.empty()) - It prints whether the stack is empty or not(True/False).
print(lis2.full()) - It prints whether the stack is full or not(True/False).

Output:

Thank you.